Tree Implementation in Java

In this article, we will provide a custom implementation of Tree data structure in Java. We will discuss a special case of Tree, i.e.- Binary Search Tree(BST). We will perform multiple tree operations such as insert(), findMin(), findMax() and search() in a BST using Java.

The below tree implementation will be based on the linked list implementation. You can check out linked list implementation in Java here.

What is Tree

Tree is a non-linear data structure for representing the hierarchical data structure in a graphical form. It is similar to a linked list but instead of each node pointing simply to the next node in a linear fashion, each node points to a number of nodes.

Tree Terminologies

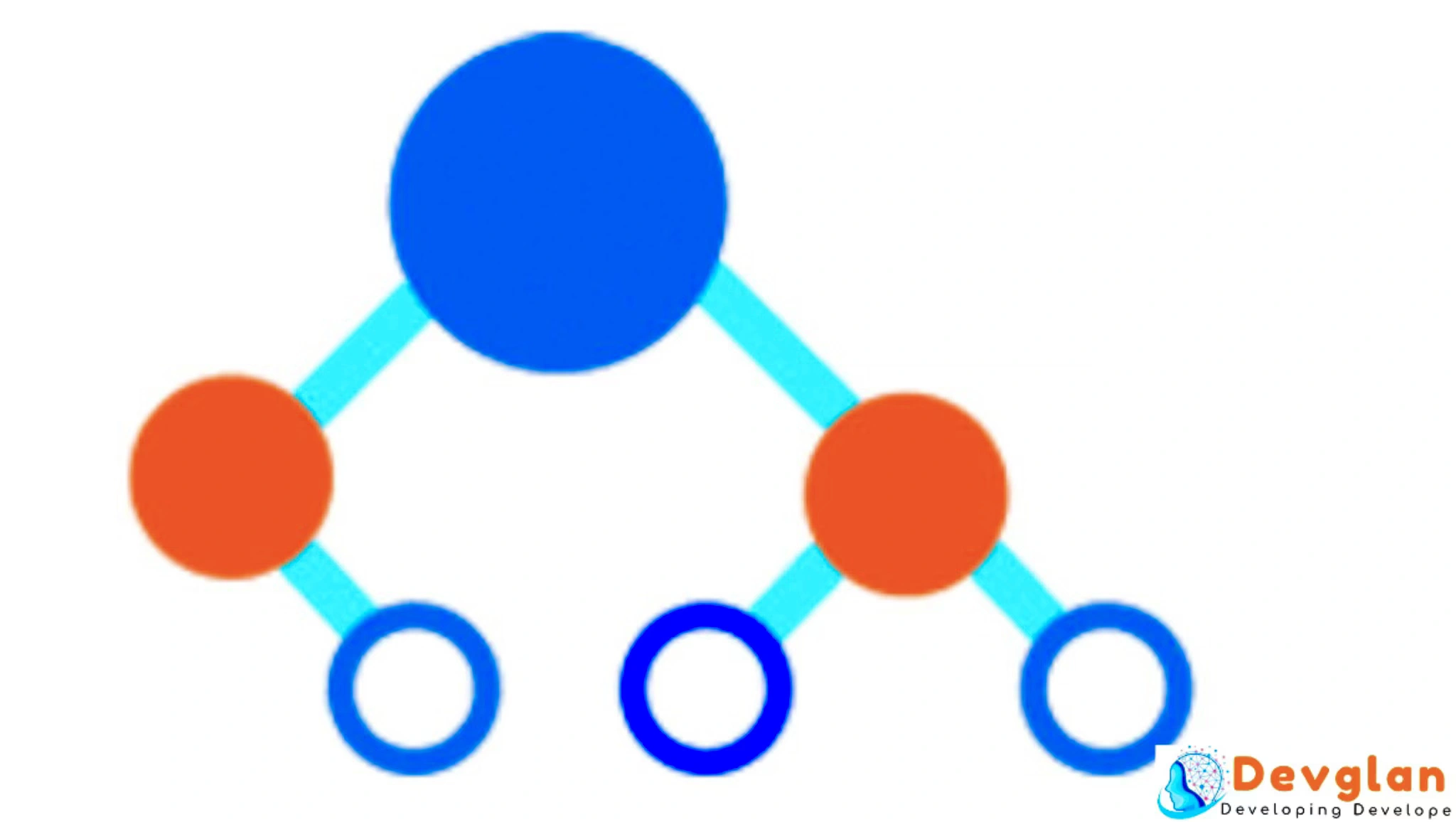
The root of a tree is the node with no parents. A is the root node.

An edge refers to the link from parent to child.

A node with no children is called leaf node. D, E, F, G, and I are leaf nodes.

B is parent of node D and E. Similarly, C is parent of F, G and H.

A is ancestor of D and E.

D and E are descendants of A.

C is sibling of B. Similarly, D and E are siblings.

D and E are the children of B.

A, B, C and H are internal nodes.

The depth(level) of E is 2.

The height of the tree is 3.

The degree of the node B is 2.

Binary Trees

A tree is called binary tree if each node has at max 2 children. It can have 0, 1 or 2 chidren. Empty tree is also a valid binary tree.

A binary tree is called strict binary tree if each node has exactly two chidren or no children.

A binary tree is called full binary tree if each node has exactly two children and all leaf nodes are at same level.

A binary tree is called complete binary tree if all leaf nodes are at height h or h - 1 meaning every level, except possibly the last, is completely filled.

Binary Tree Properties

Let us assume that the height of the tree is h and the root node is at height zero.

Th number of nodes n in a full binary tree is 2^h+1 - 1.

The number of nodes n in a complete binary tree is between 2^h and 2^h+1 - 1.

The number of leaf nodes in a full binary tree is 2^h.

The number of internal nodes in a full binary tree is 2^h - 1.

The height of a tree of n nodes is log2(no of leaves).

What is Binary Search Tree

As we know, a binary tree is a special tree in which each node has zero child, one child or two children. Empty tree is also a valid binary tree. Now, Binary Search Tree(BST) is another variant of binary tree which is mainly used for searching. BST reduces the worst-case average search operations to O(logn).

BST Properties

• The left subtree of a node should contain only nodes with keys less than the nodes key.
• The right subtree of a node contains only nodes with keys greater than the nodes key.
• Both the left and right subtrees must be binary search trees.

Since, root data is always between left subtree data and right subtree data, performing inorder traversal on binary search tree produces a sorted list.

BST Node Implementation

As discussed above, each node of a BST tree can point to a max of 2 children. Hence, below is the declaration of a BST.

public class BSTNode {

    private int data;
    private BSTNode left;
    private BSTNode right;

    public BSTNode(int data){
        this.data = data;
    }

    //setters and getters

}

BST Insertions

All BST operations are recursive. The first insertion is the root node of a BST. Then based on the data, we perform recursive insert operations either in the left or right subtree. If the data to be inserted is less than node data then insert the data in the left subtree otherwise the data is inserted in the right subtree.

public BSTNode insert(BSTNode node, int data) {
        if(node == null) {
            node = new BSTNode(data);
        }else {
            if(data < node.getData()){
                node.setLeft(insert(node.getLeft(), data));
            }else if(data > node.getData()){
                node.setRight(insert(node.getRight(), data));
            }
        }
        return node;
    }

BST Search

Start with the root and keep moving left or right based on the data that is either less than or greater than the node data recursively.

public BSTNode search(BSTNode root, int data){
        if(root == null){
            return null;
        }
        while (root != null){
            if(data == root.getData()){
                return root;
            }else if(data > root.getData()){
                root = root.getRight();
            }else {
                root = root.getLeft();
            }
        }
        return null;
    }

BST Find Smallest Element

As per the BST property, the smallest element of a BST is the left-most node, which does not has the left child.

   public BSTNode findMin(BSTNode root){
        if(root == null){
            return null;
        }
        while (root.getLeft() != null){
            root = root.getLeft();
        }
        return root;
    }

BST Find Largest Element

In BSTs, the maximum element is the right-most node, which does not have right child.

public BSTNode findMax(BSTNode root){
        if(root == null){
            return null;
        }
        while (root.getRight() != null){
            root = root.getRight();
        }
        return root;
    }

Tree Traversals

The process of visiting all nodes of a tree is called tree traversal. During traversal, each node might be visited more than once but they are processed only once.

There are mainly 3 ways of a tree traversal -

• Preorder Traversal(Root, Left, Right )
• Inorder Traversal(Left, Root, Right )
• Postorder Traversal(Left, Right, Root )

We also have Level Order Traversal which is inspired from Breadth First Traversal of graph which we have discussed in our Tree traversal implementation here.

Preorder Traversal

In pre-order traversal, each node is processed before(pre) either of its sub-trees and then the left subtree and right subtree is processed subsequently. Preorder traversal is defined as follows:

• Visit the root node
• Traverse the left subtree in Preorder
• Traverse the right subtree in Preorder

public void preOrder(BSTNode root){
        if(root != null){
            System.out.println(root.getData());
            preOrder(root.getLeft());
            preOrder(root.getRight());
        }
    }

Time Complexity: O(n) and Space Complexity: O(n)

Non-Recursive Preorder Traversal

In a non-recursive traversal, a Stack is required as we need to remember the current node so that after processing the left subtree we can go to right subtree.

Process tthe currennt node and before going tto left subttree, store the current node on stack.

After processing the left subtree, pop tthe element and go to it's right subtree. Continue the process untill stack is non-empty.

public List<Integer> preOrderNonRecursive(BSTNode root){
        List<Integer> result = new ArrayList<>();
        if(root == null){
            return result;
        }
        Stack<BSTNode> s = new Stack<>();
        s.push(root);
        while (!s.isEmpty()){
            BSTNode node = s.pop();
            result.add(node.getData());
            if(node.getRight() != null){
                s.push(node.getRight());
            }
            if(node.getLeft() != null){
                s.push(node.getLeft());
            }
        }
        return result;
    }

Inorder Traversal

In Inorder traversal the root is visited between the subtrees.

• Traverse the left subtree in inorder.
• Visit the root.
• Traverse the right subtree in Inorder.

public void inOrder(BSTNode root){
        if(root != null){
            inOrder(root.getLeft());
            System.out.print(root.getData());
            inOrder(root.getRight());
        }
    }

PostOrder Traversal

In Postorder traversal, the root is visited after both the subtrees.

• Traverse the left subtree in Postorder.
• Traverse the right subtree in Postorder.
• Visit the root.

public void postOrder(BSTNode root){
        if (root != null) {
            postOrder(root.getLeft());
            postOrder(root.getRight());
            System.out.print(root.getData());
        }
    }

Full Balanced Binary Search Tree

Full balanced BST is a BST in which the difference between left subtree height and right subtree height is at most zero. This ensures that the tree is a full binary tree.

Disadvantages of Binary Search Tree

As we know, the time complexity of searching a node in a binary search tree is the height of the tree and the height of the tree is logn. But in worst case this complexity could be equal to the number of nodes present in a binary tree i.e. n as shown in below example of nodes - 4, 7, 16, 20, 37, 38, 43 and hence it could be same as a linear search.

For the rescue we have AVL and Red Black Tree.

AVL(Adelson-Velskii and Landis) Tree

An AVL tree is a binary search tree with a balanced condition: the difference between left subtree height and right subtree height is at most 1.

Conclusion

In this article, we provided a custom implementation of BST in Java performed multiple tree operations such as insert(), findMin(), findMax() and search().